Köprüye Kazınmış Bir Formül Matematik Tarihini Nasıl Değiştirdi

Matematik Tarihini Değiştiren İrlandalı Matematikçi: William Rowan Hamilton’ın Broome Köprüsü’ndeki Büyük Keşfi

İrlandalı matematikçi William Rowan Hamilton, 1843 yılında Broome Köprüsü’nde yaptığı keşif ile matematik tarihini değiştirdi. Bu makalede, Hamilton’ın kuaterniyonlar ve vektörler ile nasıl 3D dönüşleri basitleştirdiğini keşfedin.

Bir Matematikçinin İlham Anı

16 Ekim 1843 tarihinde, İrlandalı matematikçi William Rowan Hamilton, Dublin’deki Kraliyet Kanalı boyunca yürüyüş yaparken birdenbire aklına parlak bir fikir geldi. Bu fikri o kadar heyecan vericiydi ki, Hamilton çakı bıçağını çıkardı ve Broome Köprüsü’ne kazıdı.

Bu, matematik tarihindeki en ünlü yazıdır ve şu şekilde görünür:

i2=j2=k2=−1i^2 = j^2 = k^2 = -1i2=j2=k2=−1

Hamilton’ın bu keşfi, matematikçilerin bilgiyi nasıl temsil ettiğini tamamen değiştirdi. Bu buluş, köprü tasarımı, MR cihazları, rüzgar türbinleri, arama motorları programlama ve Mars’ta bir gezgin yönlendirme gibi birçok teknik uygulamayı kolaylaştırdı.

Dönen Nesneler ve Karmaşık Sayılar

Hamilton’ın çözmek istediği problem, üç boyutlu uzayda farklı yönler arasındaki ilişkiyi nasıl temsil edeceğiydi. Kuvvet ve hız gibi kavramlar yönle ilgilidir, ancak Hamilton özellikle 3D dönüşlerle ilgileniyordu.

Matematikçiler, bir nesnenin konumunu $x$, $y$ ve $z$ koordinatları ile temsil etmeyi biliyordu. Ancak bu koordinatların nesne döndüğünde ne olacağını anlamak zor ve karmaşık geometrik hesaplamalar gerektiriyordu. Hamilton, bu işlemi daha basit hale getirmek istiyordu.

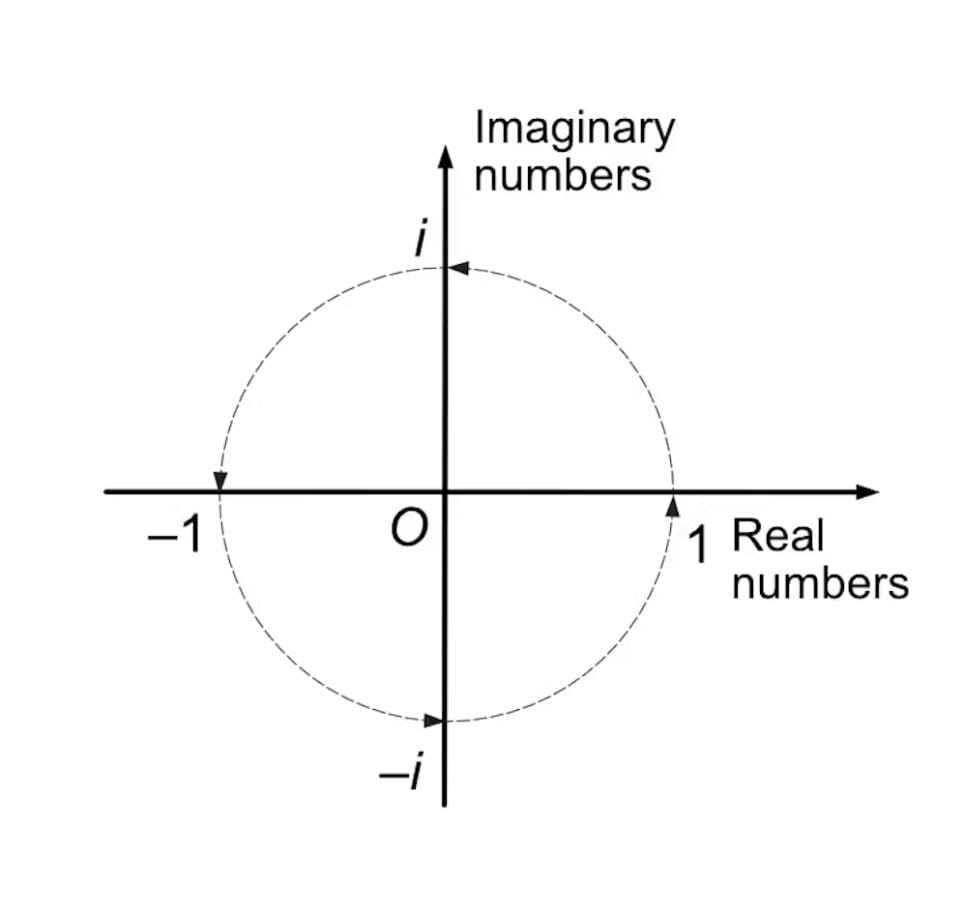
İki boyutlu dönüşleri temsil etmek için kullanılan karmaşık sayılar, Hamilton’a ilham verdi. Karmaşık sayılar, bir “gerçek” kısım ve bir “hayali” kısımdan oluşur. Hayali kısım, $i$ sayısının bir katıdır ve i2=−1i^2 = -1i2=−1 denklemi ile tanımlanır.

Üç Boyutlu ve Dört Boyutlu Düşünceler

Hamilton, iki boyutlu dönüşleri temsil eden karmaşık sayıların üç boyutlu uzaya nasıl uygulanabileceğini düşündü. İkinci bir hayali eksen olan $j$ eksenini, diğer eksenlere dik olacak şekilde ekledi. Ancak, 2D dönüşlerin mantığını üç boyuta genişletmek için yeterli değildi; dört boyutlu sayılara ihtiyaç vardı.

Bu dört boyutlu matematiksel uzayda, $k$ ekseni diğer üç eksene dik olacaktı. Hamilton’ın keşfi sonucunda ortaya çıkan denklemler şunlardı:

i²=j²=k²=ijk=−1i^2 = j^2 = k^2 = ijk = -1i²=j²=k²=ijk=−1

Kuaterniyonlar ve Vektörler

Hamilton, dört boyutlu bu sayılara “kuaterniyonlar” adını verdi. Bu sayılar, 3D uzayda geometrik dönüşleri hesaplamak için kullanılıyordu. Ancak, pratikte en önemli kısım, kuaterniyonların sadece hayali kısmını dikkate almak oldu. Hamilton, bu kısmı “vektör” olarak adlandırdı.

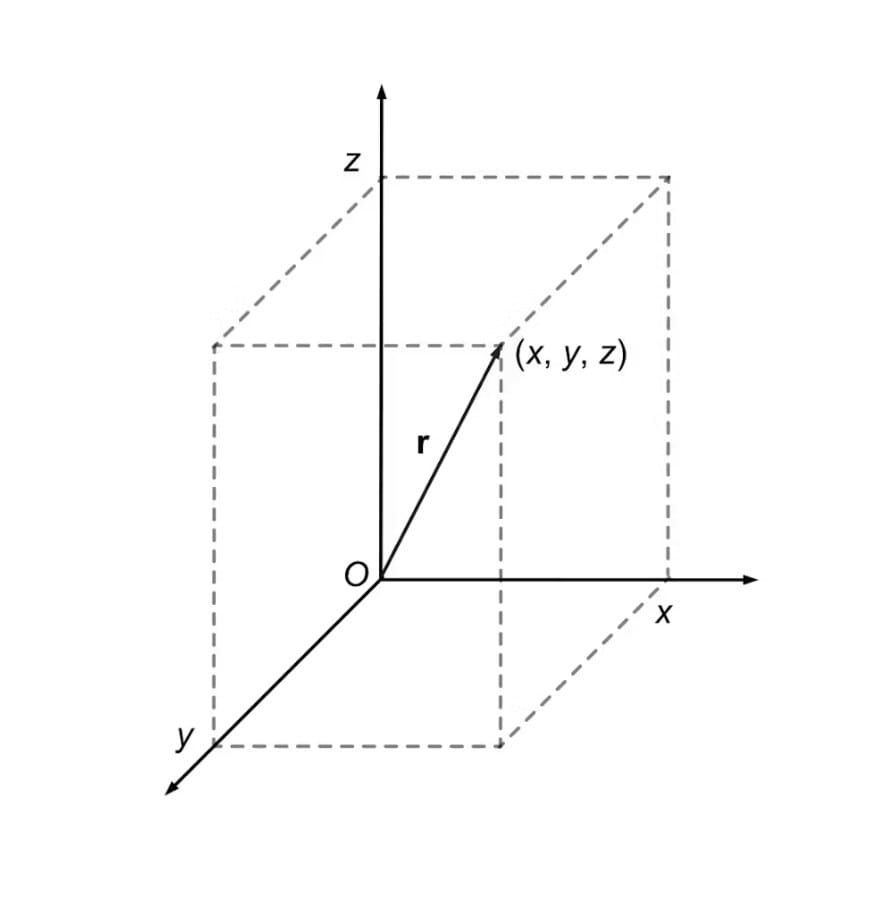
Bir vektör, kuvvet, hız veya konum gibi bir büyüklüğün hem büyüklüğünü hem de yönünü bir arada temsil eder. Örneğin, bir nesnenin konumunu (x, y, z) “orijin” noktasına göre temsil etmek için Hamilton, orijinden nesnenin konumuna doğru uzanan bir ok hayal etti. Bu ok, “konum vektörü” $xi+yj+zk$ ile gösterilir.

Hamilton, vektörlerin iki farklı çarpım yolunu tanımladı: Birincisi bir sayı üreten (bugün skaler veya nokta çarpımı olarak bilinir), ikincisi ise bir vektör üreten (vektör veya çapraz çarpım olarak bilinir). Bu çarpımlar, günümüzde elektromanyetik kuvvet formülü gibi birçok uygulamada kullanılmaktadır.

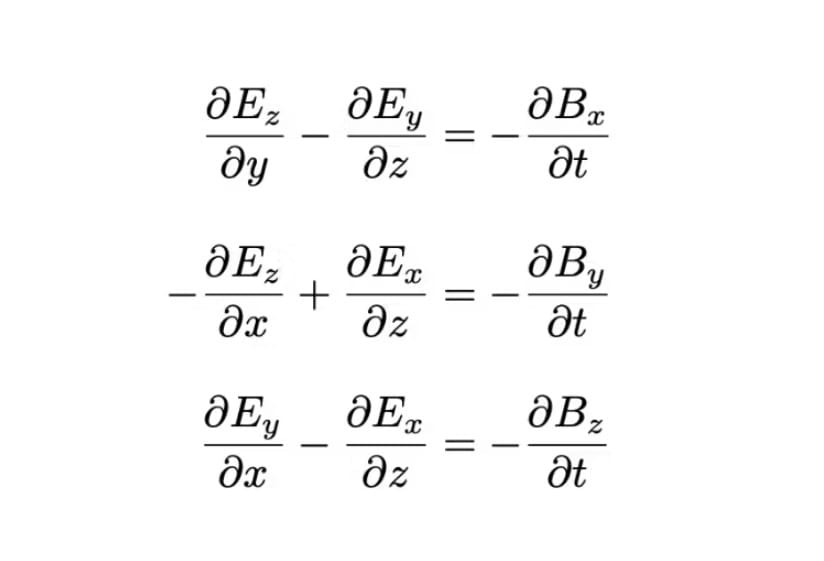
Hamilton’ın Kalıcı Mirası

Hamilton’ın keşfi, modern matematik ve fizik dünyasında büyük bir devrim yarattı. Maxwell‘in denklemleri, elektrik ve manyetik alanlar arasındaki ilişkiyi temsil etmek için vektör notasyonunu kullanarak Hamilton’ın çalışmalarının gücünü doğruladı.

Her yıl 16 Ekim’de, matematik tutkunları Hamilton Günü’nü kutlamak için onun ünlü yürüyüşünü tekrar ederler. Ancak hepimiz, bu mütevazı graffitinin teknolojik meyvelerini her gün kullanıyoruz.