E Sayısı ya da bir başka deyişle Euler Sayısı nedir?

Çok uzun bir aradan sonra yine siz sevgili okuyucularımla buluşmanın mutluluğu içerisindeyim. Bundan sonra çok güzel yazılarla daha planlı bir şekilde beraber olacağım. Bu yazıyı 14 Mart’ta yazıyorum ve öncelikle Dünya PI gününüz kutlu olsun.

Bu gün de yine PI gibi mühendislikte ve matematikte sıkça kullanılan bir sabitten, E sayısı yani  Euler sabitinden bahsedeceğiz.

2.718281828459045235360287471352662497757247…..

“e”uler sayısı matematikte, mühendislikte, doğal bilimlerde sıkça kullanılan bir sayıdır. Doğal logaritmanın tabanıdır ve irrasyoneldir. Sonlu sayıda rakamla yazılamaz. Tıpkı PI sayısı gibi…

Doğal Logaritma nedir?

Tabanı e sayısı olan logaritmalara doğal logaritma denir. log(x) veya ln(x) diye gösterilir. Savunma sanayisinde, mühendislik uygulamalarında, pH değerlerinde sık sık bu logaritma türüne başvurulur.)
Bu sayıya tarihte ilk olarak değinen Matematikçi İskoç John Napier’dir.

Ama üzerinde fazla durmamıştır. Tarihte ise bu sayıya reel olarak ilk değinen kişi Jakob Bernoulli ‘dir. Ama adını Bernoulli ‘nin çalışmalarını inceleyen Euler’den alır. Euler bu sayının ilk defa hatasız olarak 23 basamağını hesaplamıştır.

E sayısı bulunuşu

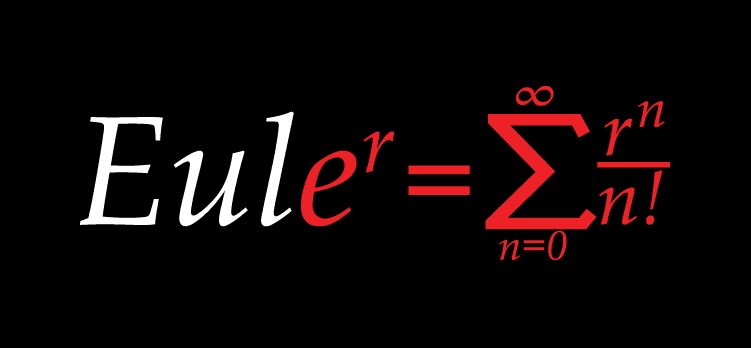
“e” sayısının bulunuşu 17.yüzyıla dayanmaktadır. Coğrafi keşiflerle beraber insanlar yeni yerler keşfetmişler, birbirleriyle daha çok etkileşime geçmişlerdir. Bunun sonucu olarak da ticaret gelişmiş, insanlar ticarete daha önem vermişlerdir.

Tabi ticaret olan yerde matematik olmazsa olmaz. Çünkü ihtiyaçtan doğan problemlere her zaman en büyük yanıtı matematik vermiştir. Bernoulli de bir bileşik faiz problemi sonucu “e” sayısını bulmuştur.

Problemden bahsedecek olursak;

Örneğin 100 TL paramız olduğunu düşünelim. Bir banka yıllık %5 bileşik faizde bankaya yatıracak olursak bir yılda paramız 105 TL olur. İkinci yılda 105*1,05 olur. Her yıl yeni fiyattan faiz işler ve para gittikçe büyür.
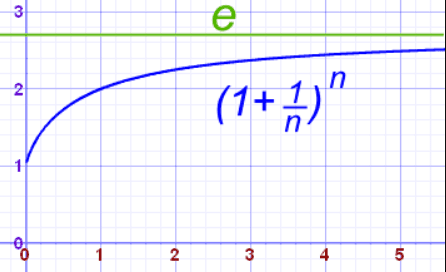
Şimdi de 1 TL paramız olduğunu düşünelim;

• **Yılda %100 faiz veren bir bankaya yatırırsa 1 sene sonra 2 lirası olur.
• **6 ayda bir %50 faiz veren bir bankaya yatırırsa 1 sene sonra 2,25 lirası olur.
• **3 ayda bir %25 faiz veren bir bankaya yatırırsa 1 sene sonra 2,44… lirası olur.
• **Ayda bir %8,33… faiz veren bir bankaya yatırırsa 1 sene sonra 2,6130… lirası olur.
• **Ve aynı şekilde haftada bir işleyen faiz sonunda 1 sene sonra 2,6925… lirası olur.
• **Her gün işleyen faizi hesapladığımızda ise 1 sene sonra 2,71453… lirası olur.

Bunu formüle dökmeye çalıştığımızda karşımıza;

n’e 10.000, 100.000 gibi çok büyük değerler verdiğinizde (10.000 için 2.71815, 100.000 için 2.71827) e sayısına yaklaşmış olursunuz. Burada n değeri faiz süresidir.
Faiz süresiyle beraber sonsuza giderken bu formülün limitini aldığımızda bize “e” sayısını verir.

Bu problem gibi başka bir problem de şapka problemidir. Bir restorana giren ve girişte şapkalarını vestiyere bırakan n tane müşteri düşünelim. Vestiyer, şapkalara etiket takmayı unutunca hangi şapkanın hangi müşteriye ait olduğunu unutuyor, ve çıkışta şapkasını isteyen her müşteriye rastgele bir şapka seçip veriyor. Bu durumda, n müşteriden hiçbirinin kendi şapkasını almaması olasılığı, aşağıdaki toplama eşittir:

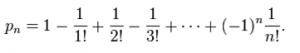
Buradaki “e” sayısı büyüdükçe toplam değeri 1 / e sayısına yaklaşacaktır. “e” sayısı ile PI sayısı arasında da çok ilginç bir bağlantı vardır. Biliyorsunuz ki Pisagor Bağıntısı bize dik üçgenlerde kısa kenarların karelerinin toplamının, uzun kenarın karesine eşit olduğunu söyler.
yani;
a2 = b2 + c2
e sayısı ile pi sayısı arasında da üçüncü bir sabitle beraber “FI (Altın Sabiti, Bunun için altın oran yazımı okuyabilirsiniz.)” sabiti arasında şöyle güzel bir ilişki vardır.

Aynı zamanda;

Bu formül Euler Denklemleri ‘nden birisidir. Ve bu formül sayesinde biz evimizde radyo dinleyebiliyoruz. Müzik dinleyebiliyoruz. Frekanslar üzerinde oynamalar yapabiliyoruz.

Matematiğin gölgesinde dinlenmeniz dileğiyle,

Bizimle Kalın,

Bilimle Kalın…