Diferansiyel Denklem Nedir, Diferansiyel Denklemler Nelerdir?

Diferansiyel denklem, matematikte içerisinde türevleriyle bir veya daha fazla fonksiyon barındıran bir denklemdir. Fonksiyonun türevleri bir noktada fonksiyonun değişim oranını belirler. Genellikle fizik, mühendislik, biyoloji gibi alanlarda kullanılmaktadır.

İçindekiler

Diferansiyel denklemleri kim icat etti sorusuna cevap ararsak bu denklemler, Isaac Newton ve Gottfried Leibniz tarafından bulundu. Fiziksel nesnelerin koordinatlarını, hızlarını ve ivmelerini hesaplamanın gerekli olduğu mekanik alanlardan, ortaya çıkmıştır.

Diferansiyel denklemi çözmenin en kolay yollarından bir tanesi açık formüller kullanmaktır.

Diferansiyel Denklem Nedir?

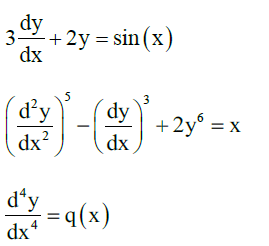
difersaniyel denklem terimi

Diferansiyel denklem, bir veya daha fazla terim ve bir değişkenin (bağımlı değişken) diğer değişkene göre türevlerini içeren bir denklemdir.

dy/dx = f(x)

Burada “x” bağımsız bir değişkendir ve “y” ise bağımlı bir değişkendir
Örnek olarak, dy/dx = 5x

Diferansiyel denklem, içerisinde kısmi türev veya adi türev içerir. Türev değişim oranını temsil ederken, diferansiyel denklemi de devamlı olarak çeşitlenen bir miktarın bir diğer miktar ile arasındaki ilişkiyi tanımlar.

Diferansiyel Denkleminin Basamağı

Diferansiyel denkleminin basamağı türevin denklem içerisinde sunduğu en yüksek basamaktır. Örnek verecek olursak.

dy/dx = 3x + 2, denklemin basamağı 1’dir.
(d2y/dx2)+ 2 (dy/dx)+y = 0, basamak 2’dir.
(dy/dt)+y = kt. Basamak 1’dir.

Birinci Basamak Diferansiyel Denklem

İlk örnekte görüldüğü üzere, derecesi 1’e eşit olan bir birinci basamak denklemi. Türev formunda olan bütün doğrusal denklemler ilk basamakta. Yalnızca dy/dx gibi birinci türevi bulunduruyor, ki burada da x ve y iki değişken ve şöyle temsil edilir:

dy/dx = f(x, y) = y’

İkinci Basamak Diferansiyel Denklem

İkinci basamak türevini dahil eden denklem, ikinci basamak diferansiyel denklemidir. Şu şekilde temsil edilir;

d/dx(dy/dx) = d2y/dx2 = f”(x) = y”

Diferansiyel Denklemin Derecesi

Diferansiyel denklemin derecesi en yüksek basamaklı türevin gücüdür. Orijinal denklemin polinom denklemi formunda y’,y”, y”’ türevleri ve benzeri şekilde temsil edilmesidir.

(d2y/dx2)+ 2 (dy/dx)+y = 0 bunu differansiyel denklem olarak ele alın, o zaman buradaki denklemin derecesi 1’dir.

Aşağıda daha fazla örneklendirecek olursak:

dy/dx + 1 = 0, derecesi 1’dir
(y”’)3 + 3y” + 6y’ – 12 = 0, derecesi 3’dür
(dy/dx) + cos(dy/dx) = 0; y′ de olan bir polinom denklemi değildir ve bu tarz bir diferansiyel denklemin derecesi tanımlanamaz.

Not: Diferansiyel denklemin derecesi ve basamağı (tanımlandıysa) her zaman pozitif tam sayıdır.

Diferansiyel Denklemlerin Türleri

Diferansiyel denklemler birkaç türe ayrılabilirler

Adi Diferansiyel Denklemler
Kısmi Diferansiyel Denklemler
Doğrusal Diferansiyel Denklemler
Doğrusal Olmayan Diferansiyel Denklemler
Homojen Diferansiyel Denklemler
Homojen Olmayan Diferansiyel Denklemler
Adi Diferansiyel Denklem

Ayrılabilir diferansiyel denklem nedir?

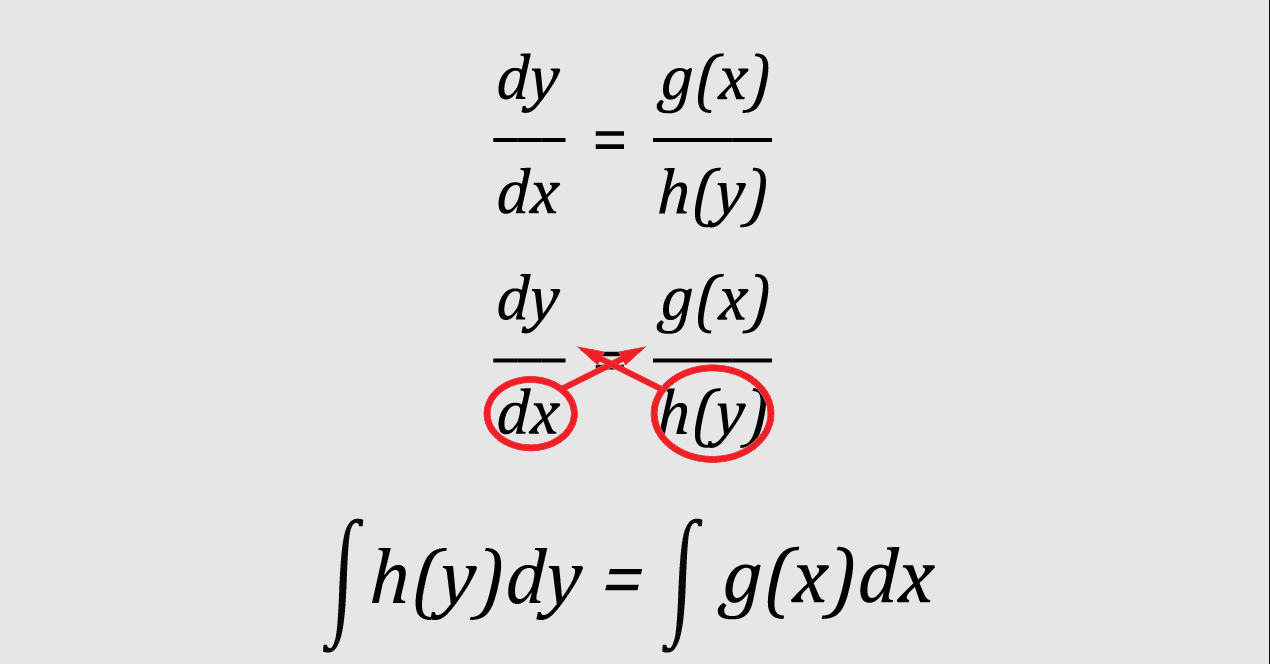
Ayrilabilir diferansiyel denklem — *Diferansiyel denklem dy/dx = f(x) g(y), değişkenlerin ayrılmasından sonra dy/g(y) = f(x) dx olarak yazılır.*

Bakacağımız ilk doğrusal olmayan birinci dereceden diferansiyel denklem türü ayrılabilir diferansiyel denklemlerdir.

Ayrılabilir bir diferansiyel denklem, aşağıdaki biçimde yazabileceğimiz herhangi bir diferansiyel denklemdir.

Adi diferansiyel denklem fonksiyon ve onun türevlerini içerir. Yalnızca bir tane bağımsız değişken ve bir veya daha fazla değişkenine göre türevler barındır.

Adi diferansiyel denklemin basamağı denklemde meydana gelen en yüksek türevin basamağı olarak tanımlanır. Adi diferansiyel denklemin genel n-th formu şu şekilde verilir;

F(x, y, y’,…., yn ) = 0

Diferansiyel Denklem Çözümleri

Diferansiyel Nasıl Hesaplanır?

Diferansiyel denklemin sağlamasını yapan fonksiyona çözüm denir. İçerisinde diferansiyel denklemin basamağı kadar keyfi sabit bulunan çözümlere genel çözüm denir. Keyfi sabitlerden ayrı olan çözümlere özel çözüm denir. Diferansiyel denklemin çözümünü bulman için 2 tane yöntem bulunmakta.

Değişkenlerin ayrılması
İntegrasyon faktörü

Değişkenlerin ayrılması, diferansiyel denklemin dy/dx = f(y)g(x) formunda olup f’nin y’ye fonksiyonu olup g’nin de yalnızca x’e fonksiyon olmasıyla yaşanır. Başlangıç değeri alıp, bu problemi 1/f(y)dy= g(x)dx olarak yeniden yazın ve sonrasında iki taraftan da birleştirin.

İntegrasyon faktörü, tekniği diferansiyel denkleminin dy/dx + p(x)y = q(x) formunda olup p ve q’nin yalnızca x’e fonksiyonu olduğunda kullanılır.

Birinci basamak diferansiyel denkleminin formu y’+ P(x)y = Q(x). P ve Q’nun x’in fonksiyonu olup aynı zamanda da y’nin birinci türevi oluyor. Yüksek basamaklı diferansiyel denklem, içerisinde kısmi veya adi türev olabilen bilinmeyen bir fonksiyonun türevidir. Herhangi bir basamakta temsil edilebilir.

Diferansiyel denklemler nerede kullanılır?

Diferansiyel denklemler matematik, fen bilimlerinde ve mühendislik gibi farklı alanlarda kullanılmaktadır. Teknik kullanımın haricinde günlük yaşantımızda da problem çözmek için kullanılır.

Bu kullanımlara bir göz atalım.

1) Diferansiyel denklemler çeşitli üstel büyüme ve azalmaları tanımlar.

2) Aynı zamanda yatırım getirisi içindeki değişimi tanımlamak için de kullanılır.

3) Tıbbi bilim alanında kanser büyümesini veya bir hastalığın vücutta yayılmasını modellemede kullanılır.

4) Yardımıyla beraber elektrik akımını da tanımlayabiliriz.

5) Ekonomistlere optimum yatırım stratejilerinde yardımcı olur.

6) Dalgaların veya bir pendulumun hareketi bu denklemleri kullanarak da tanımlanabilir.

Mühendislikte çeşitli diğer kullanımlar ise: ısı iletimi analizi, fizikte dalgaların hareketini anlamakta kullanılabilir. Adi diferansiyel denklem, mühendislik alanında köprüdeki çeşitli parçaların birbirleyile olan iletişimi bulmak için kullanılabilir.

Doğrusal Diferansiyel Denkleminin Günlük Hayattaki Örneği

Diferansiyel denklemini anlamak için basit bir örneği ele alalım. Hiç sıcak bir fincan kahvenin normal şartlar altında tutulduğunda soğuduğunu düşündünüz mü? Newton’a göre, sıcak bir bedenin soğuması T sıcaklığının ve T0 sıcaklığının çevre sıcaklık farklılıklarıyla orantılı. Bu matematikte şöyle ele alınabilir:

dT/dt ∝ (T – T0)…………(1)

Bu bir doğrusal diferansiyel denkleminin formudur.

Bir orantılılık olan Boltzmann sabitini ele alarak, yukarıdaki denklem şöyle olabilir:
dT/dt = k(T – T0) …………(2)

Burada, T vücudun sıcaklığı ve t ise zaman,

T0 çevrenin sıcaklığı

dT/dt vücudun soğumasındaki oran

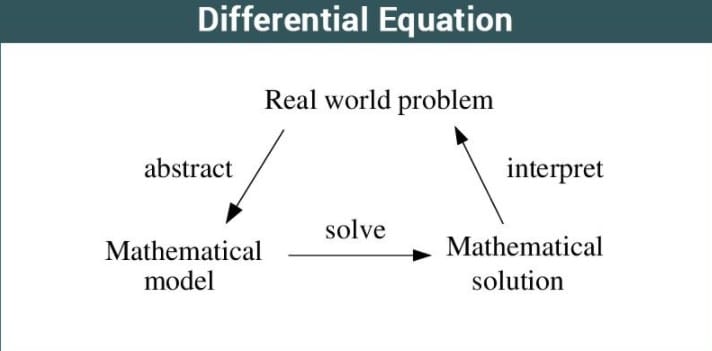
Ör: dy/dx = 3x

Burada, diferansiyel denklem içerisinde bir değişken bulunduran( bağımlı değişken, y) bir diğer değişkene de referans eden (bağımsız değişken, x) bir türev bulunduruyor. Diferansiyel denklemlerin türleri:

1. Adi denklem, içerisinde bir bağımsız değişken ve türevini bulundurur. Sıklıkla ADD( ODE) diye adlandırılır. Adi diferansiyel denklemin genel tanımı şu formdur: F, x ve y’nin bir fonksiyonu ve y’nin türevi.

F(x, y, y’ …..y^(n1)) = y (n) basamak n’nin açık bir adi diferansiyel denklemidir.
2. Bir veya daha fazla bağımsız değişken bulunduran kısmi diferansiyel denklem.

Matematik konuları hakkında daha önce hazırladığımız makaleler göz atmak isterseniz, sizler için aşağıda listesini hazırladık:

Çeviren / Faruk Ünal