Pisagor Teoremi, matematikte bir dik üçgenin hipotenüsünün karesinin, diğer iki kenarın karelerinin toplamına eşit olduğunu söyleyen bir bağıntıdır. Bu bağıntıya gerçek hayatta telli çalgılar örnek verilebilir; telin uzunluğu arttıkça titreşim de artar. Bu bağıntının adı, eski Yunan filozofu ve matematikçisi Pisagor’dan gelir. Ancak bu bağıntının Pisagor’dan çok daha önce bilindiği de düşünülmektedir. Bu bağıntının yüzlerce farklı şekilde kanıtlanabileceği bilinmektedir. New Orleans’tan iki lise öğrencisinin aşağıda göstermiş olabileceği gibi.
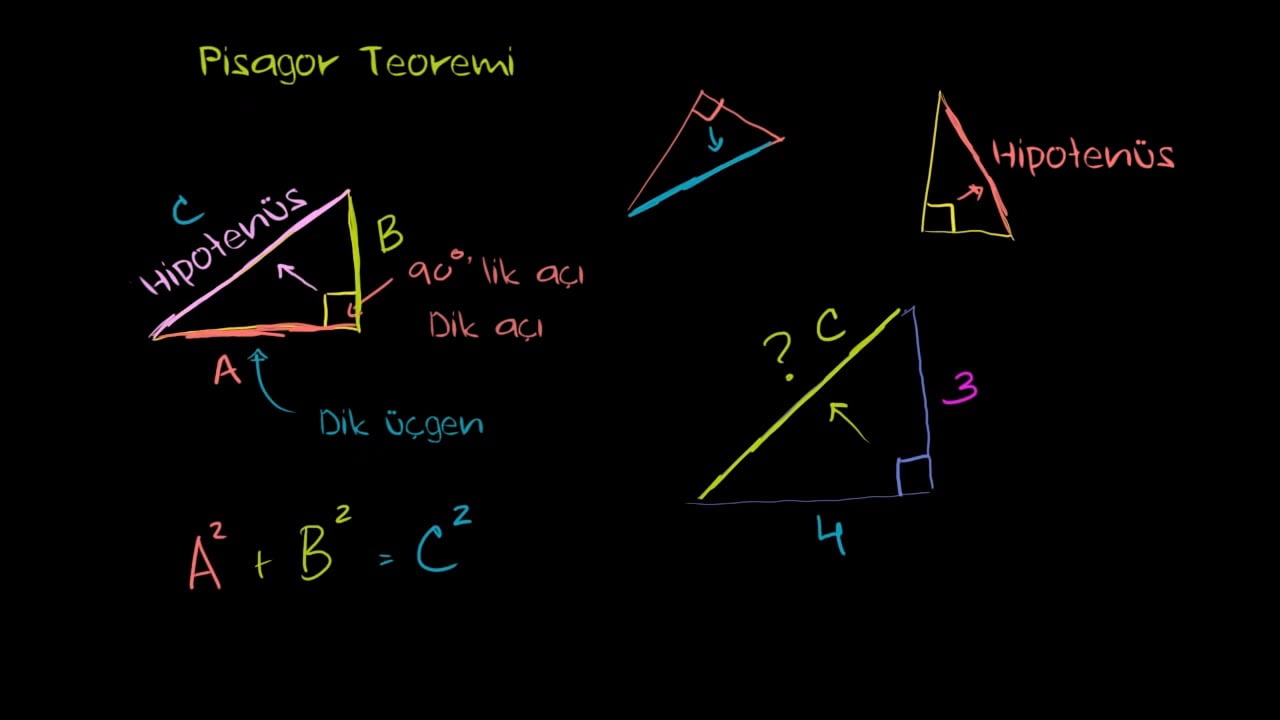
New Orleans’taki iki lise öğrencisi, Pisagor Teoremini kanıtlamak için yeni bir yöntem bulduklarını iddia ediyorlar. Bu yöntem, trigonometri kullanıyor. Trigonometri, geometrik şekillerdeki açıları ve uzunlukları inceleyen bir matematik dalıdır. Trigonometri ile Pisagor Teoremini kanıtlamak çok zordur, çünkü trigonometrinin temel kuralları zaten Pisagor Teoreminden türetilmiştir. Bu yüzden trigonometri ile Pisagor Teoremini kanıtlamaya çalışmak, mantıksal bir çelişkiye yol açabilir.
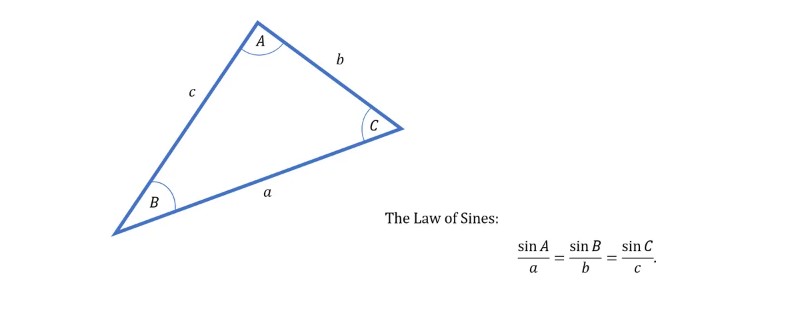
Fakat iki öğrenci, Ne’Kiya Jackson ve Calcea Rujean Johnson, bunun mümkün olduğunu gösterdiler. 18 Mart 2023’te American Mathematical Society’nin Güneydoğu Bölge Toplantısı’nda yaptıkları sunumda, Sinüs Yasası adı verilen bir trigonometrik kuraldan yararlanarak Pisagor Teoreminin yeni bir kanıtını sundular. Sinüs Yasası, herhangi bir üçgen için geçerli olan ve üçgenin kenarlarının uzunluklarını karşılarındaki açıların sinüsleriyle ilişkilendiren bir formüldür.
Öğrencilerin kanıtı şöyle işliyor: Önce bir dik üçgen çiziyoruz ve kenarlarını a, b ve c olarak adlandırıyoruz. c kenarı hipotenüstür. Sonra bu dik üçgeni aynalayarak büyük bir kare oluşturuyoruz. Bu karenin içine daha küçük dik üçgenler yerleştiriyoruz. Bu küçük dik üçgenlerin hepsi orijinal dik üçgene benziyor ve aralarındaki oran sabit. Sonra bu küçük dik üçgenlerin hipotenüslerini toplayarak x ve z adını verdiğimiz iki yeni uzunluk elde ediyoruz.
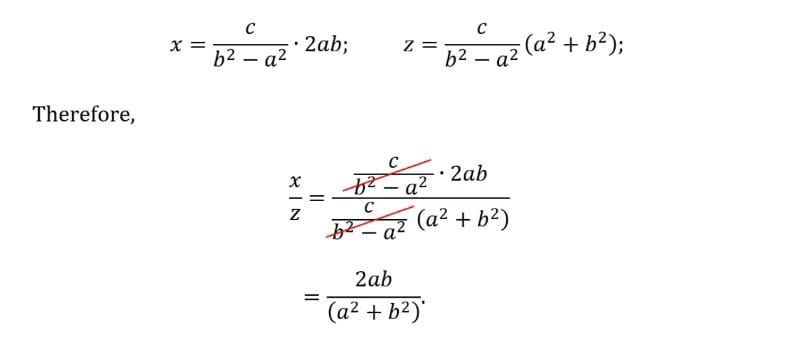
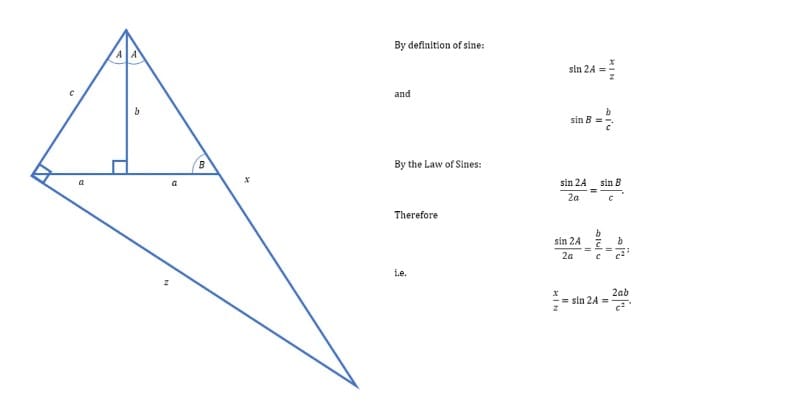
Burada x ve z’nin formüllerini bulmak için sonsuz geometrik seriler kullanıyoruz. Sonra x/z’nin sin(2A) ile eşit olduğunu görüyoruz. Burada A açısı orijinal dik üçgenin a kenarına karşı olan açısıdır. Sinüs Yasasını büyük kareye uygulayarak sin(2A)’nın da 2ab/c2 ile eşit olduğunu görüyoruz.
Bu bize şu eşitliği veriyor:
x/z = 2ab/c2
Bu eşitliği düzenleyerek şunu elde ediyoruz:
c2 = a2 + b2
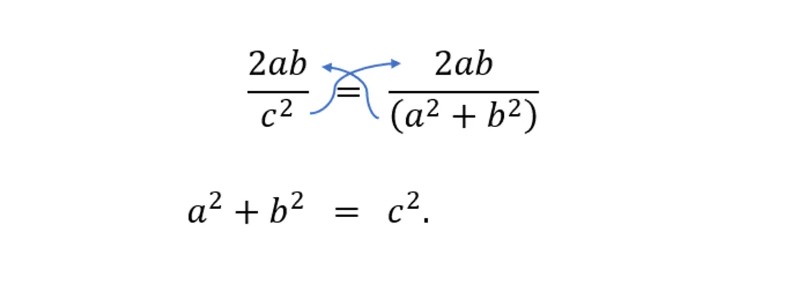
Bu da Pisagor Teoreminin kendisidir.
Bu kanıt matematik dünyasında büyük ilgi uyandırıyor. Çünkü bu kanıtın sadece Sinüs Yasası ve açı-açı teoremi gibi Pisagor Teoreminden bağımsız olan kurallara dayandığı söyleniyor. Kanıt henüz resmi olarak yayınlanmadığı için tam olarak doğrulanması gerekiyor. Ancak öğrenciler çalışmalarını yayınlamaları için teşvik ediliyorlar.
Öğrenciler ise yaptıkları işten gurur duyuyorlar. Johnson, “Böyle bir şey yapabildiğimiz için çok mutluyum. Genellikle bunu yapabilecek kişiler yetişkinlerdir” dedi.
Çeviren: Barış ARICAN




Ee biz bunu zaten liseden biliyoruz