Pi sayısı (π), matematik ve bilim dünyasında önemli bir yere sahip olan, dairenin çevresinin çapına oranını ifade eden irrasyonel bir sayıdır. Yaklaşık olarak 3.14159 değerine sahip olan pi, birçok matematiksel ve bilimsel hesaplamada kullanılır. Pi sayısı, tarihin en eski zamanlarından günümüze kadar birçok medeniyet ve bilim insanı tarafından incelenmiş ve hesaplanmıştır. Bu makalede, pi sayısının tarihi, matematiksel özellikleri, hesaplama yöntemleri ve uygulamaları ele alınacaktır.
Pi Sayısının Tarihi
Antik Dönem
Babil ve Mısır Medeniyetleri
Pi sayısının tarihi, antik uygarlıklara kadar uzanmaktadır. İlk pi hesaplamaları, M.Ö. 1900-1600 yıllarında Babil ve Mısır medeniyetlerinde görülmüştür. Babil tabletlerinde pi, 3.125 olarak hesaplanırken, Mısır’da Rhind Papirüsü’nde pi, yaklaşık 3.1605 olarak hesaplanmıştır. Bu medeniyetler, pi sayısını çeşitli mühendislik ve astronomik hesaplamalarda kullanmışlardır.
Yunan Matematiği
Pi sayısının daha kesin hesaplamaları, antik Yunan matematikçileri tarafından yapılmıştır. Arşimet, M.Ö. 250 civarında pi’yi, dairenin çevresini içine çizilen ve dışına çizilen çokgenlerin çevreleri arasında kıyaslayarak 3.1408 ile 3.1429 arasında bir değer olarak hesaplamıştır. Arşimet’in bu yöntemi, pi sayısının hesaplanmasında uzun yıllar boyunca temel yöntem olarak kullanılmıştır.
Ortaçağ ve İslam Dünyası
İslam Matematikçileri
Ortaçağ döneminde, İslam dünyasında yaşayan matematikçiler de pi sayısının hesaplanmasına önemli katkılar sağlamışlardır. Özellikle, El-Biruni ve İbn-i Sina, pi sayısının daha hassas hesaplamalarını yapmışlardır. İbn-i Sina, pi’yi 3.1416 olarak hesaplamıştır. Bu dönemde yapılan çalışmalar, matematiksel analiz yöntemlerinin gelişmesine de katkıda bulunmuştur.
Modern Dönem
17. ve 18. Yüzyıllar
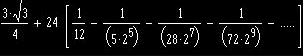
Modern dönemde, pi sayısının hesaplanması, matematiksel analiz ve bilgisayar teknolojilerinin gelişimi ile birlikte büyük bir hız kazanmıştır. 17. yüzyılda, John Wallis ve Isaac Newton gibi matematikçiler, pi sayısının hesaplanması için sonsuz seriler geliştirmişlerdir. Wallis, pi sayısını bir sonsuz çarpanlar serisi olarak ifade etmiş, Newton ise pi’yi hesaplamak için binom serisini kullanmıştır.
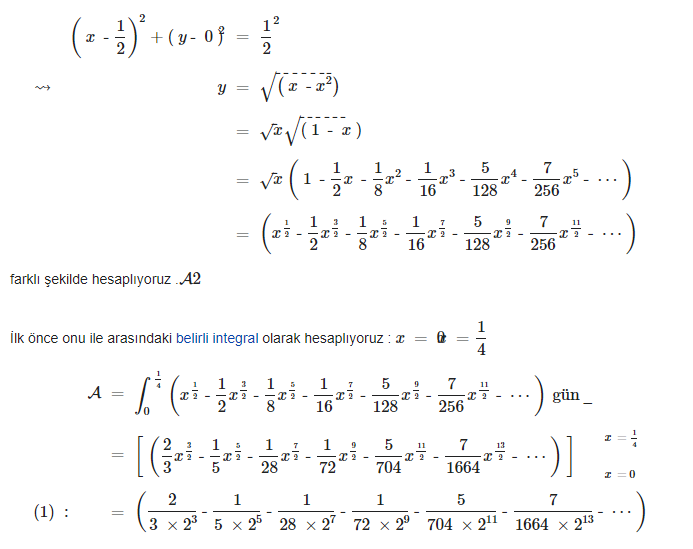
19. ve 20. Yüzyıllar
19. yüzyılda, pi sayısının hesaplanması için daha hassas yöntemler geliştirilmiştir. 1882 yılında, Ferdinand von Lindemann, pi’nin transandant olduğunu kanıtlayarak, pi sayısının hesaplanmasının sınırlarını belirlemiştir. 20. yüzyılda, bilgisayarların kullanılmasıyla birlikte pi sayısı milyarlarca basamağa kadar hesaplanmıştır. Bu dönemde, pi sayısının hesaplanması için çeşitli algoritmalar ve yazılımlar geliştirilmiştir.
Pi Sayısının Matematiksel Özellikleri

İrrasyonellik ve Transandantlik
Pi sayısı irrasyonel bir sayıdır, yani kesirli bir sayı olarak ifade edilemez. Bu durum, pi sayısının ondalık kesirinin sonsuz ve tekrar etmeyen bir dizilimde olması anlamına gelir. Johann Lambert, 1768 yılında pi’nin irrasyonel olduğunu ispatlamıştır. Daha sonra, Ferdinand von Lindemann, 1882 yılında pi’nin transandant olduğunu, yani bir polinom denkleminin kökü olmadığını kanıtlamıştır. Bu özellik, pi’nin tam olarak hesaplanamayacağını ve tam bir değere sahip olamayacağını gösterir.
Pi’nin Ondalık Genişlemesi
Pi sayısının ondalık genişlemesi, sonsuz sayıda basamaktan oluşur ve bu basamaklar rastgele gibi görünür. Ancak, bu basamakların diziliminde belirli bir düzen veya tekrar eden bir yapı bulunmaz. Pi sayısının ilk birkaç basamağı 3.141592653589793 olarak bilinir. Bilgisayarlar sayesinde pi sayısının trilyonlarca basamağı hesaplanmıştır ve bu hesaplamalar devam etmektedir.
Matematiksel Seriler ve Pi
Pi sayısının hesaplanmasında kullanılan birçok matematiksel seri vardır. Gregory-Leibniz serisi, pi/4 = 1 – 1/3 + 1/5 – 1/7 + … şeklinde ifade edilir. Bu seri, pi sayısının hesaplanmasında kullanılır ve yeterli terim sayısı kullanıldığında oldukça hassas sonuçlar elde edilir. Başka bir örnek, Machin formülüdür: pi/4 = 4*arctan(1/5) – arctan(1/239). Bu formül, pi’nin hesaplanmasında oldukça etkili bir yöntemdir.
Pi Sayısının Hesaplama Yöntemleri
Arşimet Yöntemi
Arşimet, pi sayısını hesaplamak için çokgenler yöntemini kullanmıştır. Bu yöntemde, bir dairenin içine ve dışına çizilen çokgenlerin çevre uzunlukları hesaplanarak pi sayısının yaklaşık değeri bulunur. Arşimet, bu yöntemi kullanarak pi’yi 3.1408 ile 3.1429 arasında bir değer olarak hesaplamıştır. Bu yöntem, pi sayısının hesaplanmasında uzun yıllar boyunca temel yöntem olarak kullanılmıştır.
Sonsuz Seriler
Sonsuz seriler, pi sayısının hesaplanmasında önemli bir rol oynamaktadır. Gregory-Leibniz serisi, yukarıda belirtilen örneklerden sadece biridir. Ayrıca, Euler’in pi sayısını hesaplamak için kullandığı seriler de bulunmaktadır. Euler, pi²/6 = Σ(1/n²) formülünü kullanarak pi’nin hesaplanmasında önemli bir katkı sağlamıştır.
Monte Carlo Yöntemi
Monte Carlo yöntemi, pi sayısının hesaplanmasında kullanılan istatistiksel bir yöntemdir. Bu yöntemde, rastgele noktalar bir dairenin içine ve dışına yerleştirilir ve bu noktaların oranı kullanılarak pi sayısının yaklaşık değeri hesaplanır. Bu yöntem, özellikle bilgisayarların kullanımı ile birlikte popüler hale gelmiştir. Monte Carlo yönteminin avantajı, büyük veri setleri ve karmaşık sistemler üzerinde uygulanabilmesidir.
Bilgisayar Tabanlı Yöntemler
Bilgisayarların gelişimi ile birlikte, pi sayısının hesaplanması büyük bir hız kazanmıştır. Modern algoritmalar ve süper bilgisayarlar sayesinde pi sayısının trilyonlarca basamağı hesaplanmıştır. Örneğin, 2020 yılında, Timothy Mullican, pi sayısını 50 trilyon basamağa kadar hesaplamıştır. Bilgisayar tabanlı yöntemler arasında Bailey-Borwein-Plouffe (BBP) algoritması ve Gauss-Legendre algoritması gibi ileri düzey algoritmalar bulunmaktadır.
Pi Sayısının Uygulamaları

Matematik ve Geometri
Pi sayısı, matematik ve geometri alanında birçok uygulamaya sahiptir. Özellikle, daire ve küre gibi geometrik şekillerin hesaplamalarında kullanılır. Örneğin, bir dairenin çevresi C = 2πr ve alanı A = πr² formülleri ile hesaplanır. Benzer şekilde, bir kürenin hacmi V = 4/3πr³ ve yüzey alanı A = 4πr² formülleri ile bulunur. Bu formüller, pi sayısının temel geometrik hesaplamalarda ne kadar önemli olduğunu göstermektedir.
Fizik ve Mühendislik
Pi sayısı, fizik ve mühendislik alanında da önemli bir rol oynar. Özellikle, dalga hareketleri, harmonik osilatörler ve elektrik devreleri gibi konularda pi sayısı kullanılır. Örneğin, bir sarkaç hareketinin periyodu, T = 2π√(L/g) formülü ile hesaplanır. Ayrıca, pi sayısı, Fourier dönüşümleri ve sinüs dalgaları gibi matematiksel araçlarda da sıkça yer alır. Bu araçlar, mühendislik uygulamalarında sinyal işleme, akustik ve elektromanyetik dalgalar gibi alanlarda kullanılır.
Bilgisayar Bilimleri ve Kriptografi
Pi sayısı, bilgisayar bilimleri ve kriptografi alanında da çeşitli uygulamalara sahiptir. Özellikle, rastgele sayı üreteçleri ve şifreleme algoritmalarında pi sayısı kullanılır. Pi sayısının basamakları, rastgelelik ve karmaşıklık sağlamak amacıyla çeşitli algoritmalarda kullanılmaktadır. Kriptografi alanında, pi sayısının irrasyonel ve sonsuz basamaklı olması, güvenli anahtar üretimi ve şifreleme tekniklerinde avantaj sağlar.
Diğer Uygulamalar
Pi sayısı, ayrıca, biyoloji, ekonomi ve sanat gibi çeşitli alanlarda da kullanılır. Örneğin, DNA sarmalının yapısında pi sayısının rolü vardır. DNA çift sarmal yapısı, pi sayısının geometrik özelliklerinden yararlanarak belirli bir simetri ve düzen oluşturur. Ekonomide, pi sayısı, finansal modellerde ve risk analizlerinde kullanılabilir. Sanatta ise, pi sayısının geometrik ve estetik özellikleri, çeşitli sanat eserlerinde ilham kaynağı olmuştur. Özellikle, daire ve spirallerin kullanıldığı sanat eserlerinde pi sayısının etkisi görülmektedir.
Pi Sayısının Popüler Kültürdeki Yeri
Pi Günü
Pi sayısı, popüler kültürde de önemli bir yer tutar. Özellikle, Pi Günü (14 Mart), pi sayısının anıldığı ve kutlandığı bir gün olarak bilinir. Dünya Pi Günü, ilk olarak 1988 yılında San Francisco Exploratorium’da fizikçi Larry Shaw tarafından kutlanmıştır. 14 Mart tarihi, Amerikan tarih formatında 3/14 olarak yazıldığından pi sayısının ilk üç basamağını temsil eder. Bu özel gün, dünya genelinde çeşitli etkinlikler ve yarışmalar ile kutlanmaktadır.
Kitaplar ve Filmler
Pi sayısı, çeşitli kitaplar, filmler ve şarkılarda da yer alır. Örneğin, “Pi” adlı film, pi sayısının gizemini ve matematiksel güzelliklerini konu alır. Darren Aronofsky’nin yönettiği bu film, matematiksel bir gerilim filmi olarak bilinir ve pi sayısının çevresinde dönen bir hikayeyi anlatır. Ayrıca, “Life of Pi” adlı roman ve film, pi sayısının adını taşıyan baş kahramanın yaşamını ve maceralarını konu alır.
Müzik ve Sanat
Pi sayısı, müzik ve sanat dünyasında da ilham kaynağı olmuştur. Bazı müzisyenler, pi sayısının basamaklarını müzikal notalara dönüştürerek besteler yapmışlardır. Bu tür müzik eserleri, pi sayısının matematiksel güzelliklerini ve rastgeleliğini yansıtır. Sanat dünyasında ise, pi sayısının geometrik özellikleri ve daire formu, çeşitli sanat eserlerinde kullanılmaktadır. Özellikle, soyut ve geometrik sanat akımlarında pi sayısının etkisi görülmektedir.
Pi Sayısının Geleceği
Araştırma ve Geliştirme
Pi sayısının hesaplanması ve incelenmesi, matematik ve bilgisayar bilimlerinde önemli bir araştırma konusudur. Gelecekte, daha hassas hesaplamalar ve yeni yöntemler geliştirilerek pi sayısının daha fazla basamağı keşfedilebilir. Ayrıca, pi sayısının özellikleri ve uygulamaları üzerine yapılan araştırmalar da devam edecektir. Pi sayısının farklı alanlardaki yeni uygulamaları ve keşifler, matematik dünyasında heyecan verici gelişmelere yol açabilir.
Eğitim ve Öğretim
Pi sayısı, matematik eğitiminde önemli bir konudur. Öğrenciler, pi sayısı aracılığıyla matematiksel kavramları ve hesaplamaları öğrenirler. Gelecekte, pi sayısının eğitimi ve öğretimi konusunda yeni yöntemler ve materyaller geliştirilebilir. Özellikle, dijital eğitim araçları ve interaktif öğrenme materyalleri, pi sayısının daha etkili bir şekilde öğretilmesini sağlayabilir. Ayrıca, pi sayısının tarihsel ve kültürel önemi de eğitim programlarına entegre edilebilir.
Pi sayısı, matematik ve bilim dünyasında büyük bir öneme sahiptir.
Tarihi, matematiksel özellikleri, hesaplama yöntemleri ve uygulamaları ile pi sayısı, insanlık tarihi boyunca büyük bir ilgi odağı olmuştur. Gelecekte, pi sayısının daha fazla basamağı keşfedildikçe ve pi’nin yeni uygulamaları bulunduğunda, bu sayının önemi daha da artacaktır. Pi sayısının bu eşsiz ve sonsuz gizemi, matematik ve bilim dünyasının merakını canlı tutmaya devam edecektir.
Pi sayısının matematiksel güzellikleri ve uygulama alanlarındaki çeşitliliği, onu benzersiz kılar. İrrasyonel ve transandant özellikleri, pi’nin hesaplanmasında ve araştırılmasında sürekli bir meydan okuma sunar. Bu makalede ele alınan konular, pi sayısının ne kadar derin ve kapsamlı bir konu olduğunu göstermektedir. Pi sayısının gelecekteki araştırmaları ve keşifleri, matematik ve bilim dünyasında yeni ufuklar açacaktır.