Milenyum Problemleri, matematik alanındaki en derin gizemleri temsil etmektedir. Milyoner olmak günümüz insanlarının hayallerini süsleyen büyük hedeflerden biridir. Eğer milyoner olmak istiyorsanız ve amacınıza ulaşmak için çabalıyorsanız bunun ne kadar zahmetli bir iş olduğunu da biliyorsunuzdur.
Kim Milyoner Olmak İster – Matematikten?
Amaca ulaşmak için kolay yollar aramak galiba bütün insanların yapacağı ilk tercih olabilir. Ancak bazı amaçlara ulaşmak için zor yolları da deneyebiliriz. Mesela Milenyum Problemlerinden herhangi birini çözmek size bir milyon dolar kazandırabilir.
Eğer böyle bir tercih yapacak olursanız, muhtemelen para kazanmak için mümkün olan en zor yolu seçtiğinizi size söyleyebilirim. Milenyum soruları kısmına geçmeden önce Milenyum problemleri nedir ona göz atalım.

Milenyum Problemleri Nedir ?
Milenyum problemleri, 2000 yılında Massachusetts’teki Cambridge Clay Matematik Enstitüsü günümüze kadar çözülememiş en zorlu matematik sorunlarından yedisinin bulunduğu listesiyi açıklamış ve bunlardan herhangi birini çözebilecek herkese 1 milyon dolarlık bir ödül vereceğini duyurmuştu.
Bu problemler hala matematik alanındaki en derin gizemleri temsil etmektedir. Bu sorulardan bazılarının daha iyi uzay mühendisliği, daha etkili ilaç tedavileri ve daha sert siber güvenlik şifreleme standartları gibi son derece kullanışlı pratik uygulamalara kaynaklık edebileceğini işaret ediyor. Diğer soruların ise hiçbir pratik uygulaması yoktur. Felsefi olarak insan ırkına, evrenin nasıl işlediğine dair daha ayrıntılı bir bakış açısı getirebileceği düşünülüyor.
İşte bu sözünü ettiğimiz meşhur yedi milenyum soruları:
1- Yang – Mills ve Kütle Aralığı (Çözülmedi):
Deneyler ve bilgisayar simülasyonları, Yang-Mills denklemlerinin kuantum versiyonlarına göre çözümünde bir “kütle boşluğu” olduğunu gösteriyor. Ancak bu kütle boşluğunun kanıtı yapılamamıştır.
Yang-Mills problemi nedir:
Yaklaşık yarım yüzyıl önce, Yang ve Mills, geometride de meydana gelen yapıları kullanarak temel parçacıkları tanımlamak için dikkate değer yeni bir çerçeve sundu. Yang-Mills problemi, kuantum mekaniğine ve temel parçacık fiziği anlayışımıza yönelik teorik düşünce uygulamalarının çoğunluğu için temel bir dayanaktır. Yang-Mills teorisinin çözülmesi, hem fizikte hem de matematikte temel fikirlerin tanımlanmasını sağlayacaktır.
Yang-Mills problemi, belirli bir gerçek alan için ![]() , iki nokta fonksiyonunun özelliği varsa, teorinin kütle boşluğu olduğunu söyleyebiliriz.
, iki nokta fonksiyonunun özelliği varsa, teorinin kütle boşluğu olduğunu söyleyebiliriz.
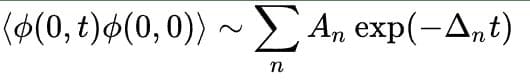
ile birlikte![]() Hamiltoniyen spektrumundaki en düşük enerji değeri ve dolayısıyla kütle boşluğudur. Diğer alanlara genellemesi kolay olan bu miktar, genellikle kafes hesaplamalarında ölçülen şeydir.
Hamiltoniyen spektrumundaki en düşük enerji değeri ve dolayısıyla kütle boşluğudur. Diğer alanlara genellemesi kolay olan bu miktar, genellikle kafes hesaplamalarında ölçülen şeydir.
2- Riemann Hipotezi (Çözülmedi):
Riemann Hipotezi Nedir?
Riemann Hipotezi çözüldü mü? Hayır.
Asal sayı teoremi, asalların ortalama dağılımını belirler. Riemann hipotezi bize ortalamadaki sapma hakkında bilgi verir. Riemann’ın 1859 yılında yayınlanan makalesinden formüle edildiğinde, zeta fonksiyonunun tüm ‘açık olmayan’ sıfırlarının gerçek kısımları 1/2 ile karmaşık sayılardır.
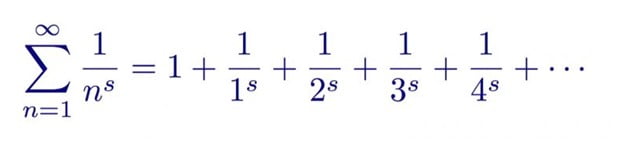
Riemann ne buldu?
Georg Friedrich Bernhard Riemann (17 Eylül 1826 – 20 Temmuz 1866), analiz ve diferansiyel geometri dalında çok önemli katkıları olan Alman matematikçidir. Söz konusu katkılar daha sonra izafiyet teorisinin geliştirilmesinde önemli rol oynamıştır.
3- P, NP’ye karşı Problemi (Çözülmedi):
“Bir sorunun çözümünün doğru olduğunu kontrol etmek kolaysa, soruyu çözmek de kolay mıdır? P-NP sorusunun özü budur. NP problemlerinin tipik hali “Hamiltonian Yolu” problemidir.
P ve N şehirlerini ziyaret etme durumunda, N şehrine gittikten sonra güzergahta P var. bir şehri iki kez ziyaret etmeden bu güzergahı nasıl tamamlayabiliriz? Bana bir çözüm verirseniz bunun doğru olup olmadığını kolayca kontrol edebilirim. Ancak bu kadar kolay bir çözüm bulamıyorum.”
4- Navier–Stokes Denklemleri (Çözülmedi):
Bu soru sıvılar ve gazlar gibi akışkanların hareketini tanımlamaya yarayan bir dizi denklemden oluşmaktadır. Bu denklemler en temel ve bilinen şeyler için bir kanıt olmamasından dolayı oluşturulmuştur.
Basit gerçekler üzerine çözümler var mı ve bu çözümler benzersiz mi?
Neden bir kanıt arıyoruz?
Çünkü bir kanıt sadece bir güvence vermekle kalmaz, aynı zamanda olaya veya duruma bir anlayış katar.
Bu denklemler en kullanışlı denklemlerin başında gelmektedirler. Çünkü, gerek akademik gerekse ekonomik birçok fenomenin fiziğini açıklamaktadır. Hava akımları ve okyanus akıntılarının, boru içindeki su akışının, galaksideki yıldız hareketlerinin, kanat etrafındaki hava akımlarının modellenmesinde ve hesaplarında sıkça kullanılırlar.
5- Hodge Kestirimi (Çözülmedi):
Hodge kestirimi nedir?
Bu varsayımın cevabı, bir cebirsel denklem sisteminin çözüm kümesi topolojisinin ne kadarının cebirsel açısından tanımlanabileceğini belirler. Hodge hesabı belirli özel durumlarda, örneğin, çözüm setinin dörtten küçük olması durumunda bilinir. Ancak dördüncü boyutta bilinmemektedir. Bizim aradığımız şey ise bilinmeyendir.
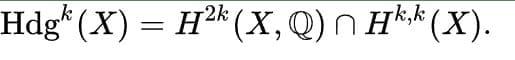
Biz buna X üzerinde 2 k dereceli Hodge sınıfları grubu diyoruz.
Hodge varsayımının modern ifadesi:
X , tekil olmayan bir kompleks projektif manifold olsun. O zaman X üzerindeki her Hodge sınıfı, X’in karmaşık alt çeşitlerinin kohomoloji sınıflarının rasyonel katsayıları ile doğrusal bir kombinasyondu. Sorunla ilgili resmi açıklama Pierre Deligne tarafından yapıldı.
6- Poincare Kestirimi (çözüldü):
Poincare Kestirimi, Dr. Grigoriy Yakovlevich Perelman tarafından çözüldü.
1904’te Fransız matematikçi Henri Poincare, üç boyutlu kürenin basit bağlanmış üç manifold ile karakterize edilip edilemeyeceğini sordu.
Bu soru Thurston’un geometrileştirme varsayımının özel bir durumuydu. Perelman’ın kanıtı, her üç manifoldun her birinin sekiz iyi anlaşılmış geometriden birine sahip bir dizi standart parçadan yapıldığını söyler.
İşte, 1 milyon dolarlık Poincare Kestirimi’nin Perelman tarafından çözümü: İndir, Yazdır.
7- Birch ve Swinnerton – Dyer Kestirimi (Çözülmedi):
Birçok deneysel kanıtla desteklenen bu varsayım, bir p eliptik eğri üzerindeki noktaların sayısını rasyonel nokta grubunun kümesi ile ilişkilendirmektedir.
İki değişkende kübik denklemler ile tanımlanan eliptik eğrilerle desteklenen ve birçok alanda ortaya çıkan temel matematiksel nesneler: Wiles’in Fermat Konjürasyonunun kanıtlaması, sayıların asal çarpanlarına ayrılması ve kriptografi (veri şifreleme).
Milenyum Problemleri ‘ni Çözmeye Ne Kadar Yakınız?

2019 yılı itibariyle sadece Poincare Kestirimi(varsayımı) çözülebildi. Bu soru Rus Matematikçi Grigoriy Perelman tarafından 2002 yılında çözüldü.
Perelman, bu soruya karşılık yazdığı cevapla Nobel Ödülünün matematik alanında eşdeğeri olan Fields Madalyasını kazandı. Profesör, şaşırtıcı bir şekilde hem Fields Madalyası’nı hem de 1 milyon dolarlık ödülü reddetti.
Görünüşe göre soruyu çözdüğünden dolayı pek memnun değildi. Poincare Kestirimi, az sayıda pratik uygulamaya sahip bulmacalardan biriydi. Sorunun temelinde tamamen kapalı bir şeklin, n sayıda boyutta küre olarak kabul edilip edilemeyeceğinin bilinmemesiydi.
Perelman, sorunun yayınlanmasının üzerinden neredeyse bir yüzyıl geçtikten sonra, basitçe birbirine bağlı tüm kapalı şekillerin çok karmaşık bir sırada da olsa kategorize edilebilecek güzel ve düzenli bir özellik kümesini paylaştığını kanıtladı.
Perelman bununla birlikte listedeki soru sayısını altıya düşürdü. 2019 yılı itibariyle dünyanın dört bir yanından gelen matematikçiler bu sorulara onlarca potansiyel çözüm sundu. Ancak bunların çoğu değerlendirilme sürecine dahi giremedi.
Milenyum problemlerinden kaç tanesi çözüldü kaçı kaldı?

Bugüne kadar çözülmüş olan tek Milenyum sorusu Grigori Perelman tarafından çözülen Poincaré varsayımıdır.
Çözülmemiş Milenyum Problemleri, Birch ve Swinnerton-Dyer varsayımı, Hodge varsayımı, Navier-Stokes denklemleri, P, NP’ye karşı Problemi, Riemann hipotezi ve Yang – Mills ve Kütle Aralığı problemleridir.
Şu an incelenmekte olan en umut verici çözümlerden ikisi Mukhtarbay Otelbayev’in Navier-Stokes problemine getirdiği çözüm önerisi ve Michael Atiyah’ın Riemann Hipotezi için geliştirdiği çözümdür. Her ikisi de gerçekten pratik uygulamalar için önemli olan sorular olarak varlığını koruyor. Umarız insanlık bu milenyum soruları bilinmezliğini en kısa sürede çözebilir.
Bunlar da ilginizi çekebilir:
- ‘160 yıllık matematik problemi çözüldü’
- Adeta Matematikle Konuşan Mimar Sinan Eserleri ve Hayatı
- Teşekkür Etmemiz Gereken Denklemler ve Denklemlerin Kullanım Alanları
- Matematikçiler Büyük Sayıların Çarpımında Yeni ve Şaşırtıcı Bir Yol Keşfetti!
- Arılar, temel matematik işlemlerini yapabilir
- Anunnakiler ilk matematiksel sistem ile evrene ilişkin şifreleri mi açığa vurmak istediler?
Yazar: Onur Can CANİKLİ





Hocam şimdi 3- P, NP’ye karşı Problemi’nde N ve P şehirlerini komşu saymadan eliptik şeklindeki dünyamızda aynı dairesel bir yol üzerinde konuşlandıralim. Bu sayede N’den başlayıp P’ye giderken yalnızca bir kez geçmiş oluruz. Mantıklı mıdır sizce de?