İnsan beyni hem mucize hem de gizemdir.
İçerisindeki alanın dörtte biri kadar sıkıştırılmış ve yaklaşık 86 milyar nöron ağı bulunur. Ancak bu ağ yapısını iyice anlayabilmek hala tartışmaya açık bir soru.
Algı ne yazık ki can sıkıcı bir konu olmaya devam ediyor: İnsan beyni sürü halinde gelen sinyalleri -fotonları, kokulu molekülleri, ses dalgalarını, derimizin üzerindeki hisleri- nasıl oluyor da zihinsel bir danışıklığa dönüştürüyor?

Sinir ağları neyi temsil eder? Çikolata kokusunu mu?
Yapılan son araştırmalar matematiğin bu soruları çözümlemeye yardımcı olabileceğini söylüyor.
Algıya dahil olan karmaşık ağları ve diğer bilişsel olayları daha iyi değerlendirebilmek için bazı araştırmacılar yüzünü hiperbolik geometriye çevirdi.
Diğer geometriler gibi bu geometri de uzay, mesafe ve bağlantılar bazında birtakım kurallara sahip ancak Öklid geometrisinin tersine hiperbolik geometri uzayın birbirine geçmesini gözler önüne serer – eğer uzay kendinden uzağa doğru bükülebilseydi, her yere bükülebilirdi.

Salk Enstitüsü Biyolojik Çalışmaları’ndan Tatyana Sharpee “Hiperbolik geometri biyoloji alanında uzun zamandır pek değer görmemiştir.” dedi. Son birkaç yıldır burun sistemi hakkındaki çalışmaları kendisini hiperbolik geometriye yönlendirdi ancak koku duyumuz sadece bir başlangıç: Sharpee, aynı yaklaşımın diğer duyularda ve işlemlerde de genelleştirilebileceğini düşünüyor.
Eğer Sharpee gibi araştırmacılar haklıysa zihni anlayabilmek için hiperbolik geometrinin doktrinlerini kucaklamaya hazırlanmamız gerekiyor.
İlginizi çekebilir: Beyinle İlgili Bilinen 10 Yanlış
‘Dipsiz Gece’nin Başlangıcı
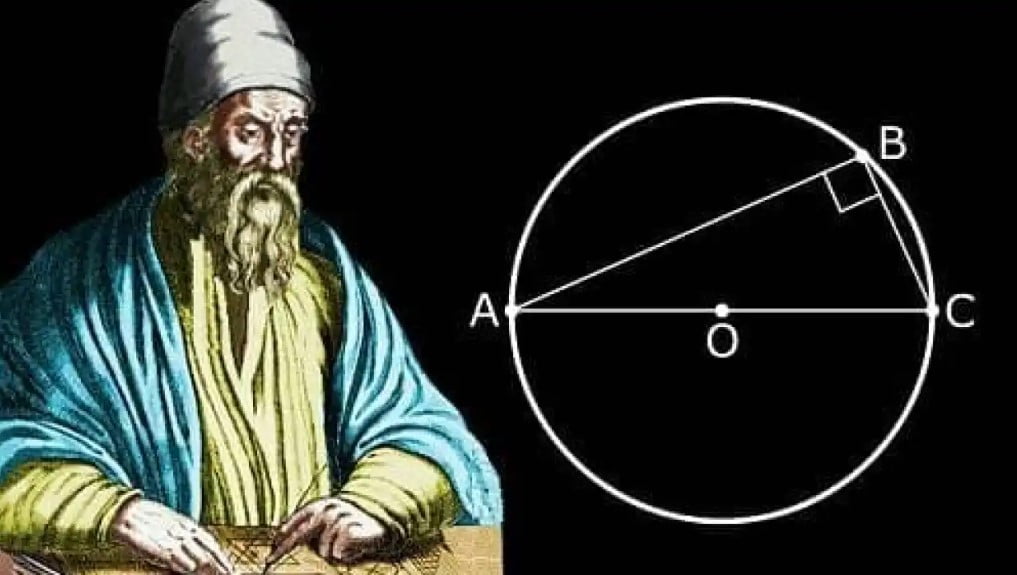
Yaklaşık 2 bin yıl önce yazılmış, “Geometrinin babası” olarak tanınan Yunan matematikçi Öklid’in bilimsel eseri ‘Elementler’i dünya olarak esas alıyoruz. Bu kurallar düz, pratik, fiziksel dünya ve günlük yaşam düzeni için oldukça yararlıdır.
Öklid geometrisi denizleri aşmamızı, gökdelenler dikmemizi ve Ferrarileri yarıştırmamıza olanak sağladı.
Ancak sorun Öklid’in beşinci postülası ile meydana çıkıyor. Orijinal formunda, düz bir çizgi diğer iki düz çizgiyle kesişiyorsa ve bu aynı taraftaki kesişimler 180 dereceden az iç açılar oluşturuyorsa diğer iki düz çizginin bir yerde buluşması gerekiyor. (Birçoğumuzun bildiği bu durumu basit ifadelerle anlatacak olursak: paralel çizgiler asla kesişmez.)
Pisagor teoremini ele almamız tamamen Beşinci postüla yüzünden ve bu durum üçgenin iç açılarının toplamının 180 derece olduğuna kanıt.
Bir postüla apaçık olmalı ancak paralel çizgi mevzusu matematikçileri can evinden vuruyor. İçten içe pek de ikna edici gözükmüyor keza Öklid bile “Elementler” in büyük bir kısmında beşinci pöstuladan bahsetmedi.
Bu soru her şeyi değiştirdi. Öklid’in Beşinci’sini hiçe saymanın sadece akıl dışı olmadığını fark ettiler. Bu durum istikrarını sürdürmeye devam eden yeni egzotik geometrilere açılan bir kapıydı.
Öklid’in “Beşinci” fikrini zayıflatmak

Öklid’in “Beşinci” fikrini zayıflatmak Carl Friedrich Gauss veNikolaiLobachevsky gibi zamanının büyük düşünürlerinin de ilgisini çekti. Dikkate değer kişilerden biri de bu yeni geometrinin kurallarını oluşturan birkaç isimden olan JánosBolyai adında gelecek vadeden Macar bir gençti.
1820’de Öklid’e karşı gelecek radikal bir plana girişti. János Öklid’in “Beşinci Postüla”sını esnetmenin Öklid dışı geometrilere yeni pencereler açacağını fark etti.
Babası Farkas hoşnutsuzluğunu matematikçilerden sık duyamayacağımız bir üslupla dile getiriyordu.
Oğluna “Tanrı aşkına, lütfen bırak şu işi.” diye yazdı.
“Ondan uçarı bir ilişkiymiş gibi tiksin. Bu iş seni tüm boş vaktinden, sağlığından, sıhhatinden ve bütün yaşam mutluluğundan yoksun bırakabilir.” Kendisi de matematikçi olan ve Gauss ile yaşamlarının sonuna kadar arkadaş kalan Farkas kendisinin de bir zamanlar Öklid’e kafa tuttuğunu belirtti. “O dipsiz geceyi ben de inceledim. Hayatımdaki tüm ışık ve neşe oracıkta gidiverdi.”
Caydırılamayan Jánosşimdilerde Öklid dışı geometri olarak adlandırdığımız alandaki kanunlara çözüm getirdi. Öklid geometrisinde bir üçgenin iç açıları toplamı 180’e kadar çıkabilir ve paralel çizgiler asla kesişmez ancak Öklid dışı geometride durum böyle değil.
Küresel geometriden bir örneğe göre eğer bir kürenin üzerine üçgen çizerseniz açıların toplamı 180’den fazla olabilir.
Hiperbolik geometri Öklid dışı geometrinin bir başka bilinen türüdür. Üç boyutlu yüzeyde havada kalan hiperbolik bir uçak düz gözükmez; daha çok bir Pringles dilimine ya da eyere benzer, her tarafa bükülebilir.
Eğer hiperbolik bir uçakta ayakta duruyorsanız, bir yöne doğru bir adım atarsanız havalanırsınız; 90 derece dönüp bir adım atarsanız alçalırsınız. Hiperbolik boşlukta üçgenin iç açıları toplamı 180 dereceden biraz daha az olabilir.
İlginizi çekebilir: İnsan Beyniyle İlgili 10 İlginç Gerçek
Bükülen Koridorlar ve Öklid Dışı Geometri
Neredeyse unutulmuş ve yüz yıl öncesine dayanan çalışmalar hiperbolik geometrinin görsel algıda bizlere yardımcı olabileceğini söylüyor. 1902 yılında Alman bilim adamı F. Hillebrand karanlık oda deneyleri yaptı.
Tam 10 yıl sonra W. Blumenfeld bu deneyi tekrarladı ve gönüllü katılımcılardan başları sabit bir şekilde karşıya doğru bakmaları istendi.
Sonrasında paralel hat üzerindeki bir dizi parıldayan ışığa baktılar, kafalarını dışarı çıkardıklarında her hattın görüş açılarından aynı uzaklıkta olduğunu fark ettiler. Deneyin sonunda bir vadinin ortasına bakıyormuş gibi hissettikleri ortaya çıktı.

Fakat bu deneyler bir paradoksu da doğurdu: Katılımcıların algıladıkları hatlar ne düz ne de paraleldi. Aksine peş peşe dizili hatlar eğriydi. 1940’larda Alman doğumlu matematikçi RudolfLuneburg paralel hatların algıda ve gerçeklikte neden değişiklik gösterdiğini açıklamada yardımcı oldu.
Luneburg, iki gözle görmenin çevremizdeki şekillerin ve konumların her ikisini de üç boyutlu bir harita olarak algılamamıza neden olduğunu fark etti. Fiziksel gerçekliğin ve gördüğümüz şeylerin bir tür çeviri aracı olan bir ölçü oluşturdu.
Luneburg ve çalışma arkadaşları algımızdaki prensiplerin yalnızca Öklid dışı olmadığı, ayrıca hiperbolik geometriyle daha iyi yansıtılacağı sonucuna vardılar.
Yıllar sonra, 1983’te bilim filozofu PatrickHeelan benzer bir şekilde hiperbolik görsel uzamının varlığını tartışmaya açtı; Heelan ayrıca Paul Cézanne, Vincent van Gogh ve Joseph Mallord William Turner gibi ressamların eserlerinde hiperbolik yapıları tasvir ettiklerine de parmak bastı.
Kokunun Geometrisi
Günümüzde bu konu hala çözülmedi. Araştırmacılar algı ağlarının yapısını incelemeye devam ediyor. Yapılan son araştırmaların bir kısmı görsel uzamın gerçekten de Öklid dışı olduğuna dair kanıtlar sundu.
2018 yılında yapılan bir çalışmada araştırmacılar Öklid dışı geometriyi kullanan insanların Öklid açısını kullananlara göre şekilleri daha gerçekçi algıladıklarını ortaya koydu.
İlginizi çekebilir: İnsanlardaki Koku Duyusu Düşündüğümüzden Daha Güçlü
Sharpee gece göğünün hiperbolik algı için ikna edici bir kanıt olduğunu belirtti. Karanlık kâinatı kubbe gibi görürüz ancak astronomik mesafeler biçimsizdir.
Çocuklar aya ulaşmaya çalışırlar çünkü ay onlara dokunabilecekleri kadar yakın oldukları hissini verir ancak “mesafeler sıkıştırılmıştır.”.
Bu durum algının hiperbolik sırlarını çözmemizde anahtar görevi görebilir: Oranları sadece geniş ve kapsayıcı ölçeklerde ortaya çıkar. “Küçük bir ölçeğin üzerindeki herhangi bükük bir geometri Öklidyendir.
Newark, New Jersey; New York City ve Nyack, New York’un oluşturduğu üçgen Öklid prensiplerine uygundur. Sharpee“Düz dünya hipoteziyle tutarlılık gösterir ancak New York’dan Londra’ya, Londra’dan Melbourne’e olan mesafeyi göz önünde bulundurursak böyle bir tutarlılıktan söz edemeyiz.” dedi.
Bu, kendisinin oluşturduğu karmaşık haritasındaki esas fikirdi. Benzer molekül yapılarına sahip koku moleküllerinin aynı algılanmasını düşünmek çok cezbedici fakat Sharpee’nin bulduğu bu değil. Sharpee ortak kokuların kimyasal yapılarını araştırdı ve deneydeki katılımcılardan benzer kokuları gruplandırmaları istendi.
Koku Kümeleri

Bulgular insan beyninin moleküler yapılardan ziyade kokuları meydana çıktıkları sıklığa göre gruplandırdığını gösteriyor. Bu koku kümelerinin haritasını oluşturduğunda Sharpee benzer biçimde oluşturulmuş moleküller arasındaki mesafenin en iyi hiperbolik geometrideki mesafe kavramıyla temsil edilebileceğini ortaya koydu.
Yaptığı çalışma beynin örgütsel yapısına bükülmüş bir uzaymış gibi yaklaşırsak bilgiyi algılamada beynin nasıl organize olduğunu daha iyi anlayabileceğimizi gösteriyor.
Hiperbolik geometri beynin karmaşık yapısını modellemede oldukça yararlı oldu. Barselona’daki fizik uzmanları bir dizi hayvan türü üzerinde beynin ağ yapısını modelledi.
Nöronların uzamsal alanda kendilerine en yakın nöronla iletişim kurmasının pek de gerekli olmadığına aksine bir dizi kuralları takip eden daha egzotik bir geometrinin geçiş ağına sahip oldukları sonucuna vardılar.
Hiperbolik uzam birkaç türün beynindeki ağ yapısını izlenebilir haritalar olarak görmemize olanak sağlıyor. Uzmanlara göre hiperbolik geometri “beynin yeni kartografisi” olarak göze çarpıyor.
Benzer bir şekilde bazı bilgisayar uzmanları hiperbolik geometrinin büyük veri kümelerini düzenlemede oldukça etkili bir rol oynayabileceğini söylüyor.
Barselona Üniversitesi’nde doktora sonrası araştırmacı olan ve çapraz türler çalışmasında yer alan Quebec Lavan Üniversitesi fizikçisi AntoineAllard “Hiperbolik geometri beynin yapısal karmaşıklığını temsil etmek için oldukça doğal bir yol.” dedi.
Yasin Osman Kara