Bu makale, Eleştirel Düşünme üzerine 3 bölümlük bir dizinin 2. Bölümüdür. 1.Bölümü ve 3. Bölümü burada bulabilirsiniz.
Her gün yüzlerce karar veriyoruz ve farkında olsak da olmasak da hepimiz kritik eleştirel düşünürüz. İşte kritik düşünce metotları.

Çapa Etkisi
Çapa etkisi genel bir zaafımız, doğuştan gelen bir kusurumuzdur. Kabaca ifade edecek olursak, bir önceki eylemde algıladığımız, etkileşime girdiğimiz veya öğrendiğimiz bir sayının gelecekteki kararlarımızı etkilemesidir.
Çapa etkisi bir bilgiyi neticeye ulaşılan süreçte çıkarım yapmak için kullanmaktır. Bu tip bir sürece aslında sıkça başvurulur ve hataların büyük oranda kaynağı olabilir.
Örneğin araştırmalar gösteriyor ki bir ifadede alakasız bir sayı verildiğinde bu sayının alakasız olduğu bilinse bile kişilerin vardığı neticeyi etkileyebiliyor.
Bir örnekle bunu gözlemleyelim. Mesela şöyle diyebilirsiniz:

‘Kilimanjaro Dağı 20.000 metre yükseklikten düşük mü yoksa fazla mı?’
Birçok kişi bu sayının abartılı olduğunu düşünecektir, ancak bu yine de bilinçaltında fikirlerini etkiliyor. 20.000 lafı geçmeden doğrudan tahminleri sorulan kişiler, bu soruyu gören kişilere kıyasla daha düşük sayılar ile tahminde bulunuyorlar.
Başka bir örnek vermek gerekirse; insanlara en ağır insanın 1000 kilodan az olup olmayacağı sorulduğunda yine buradaki 1000 sayısı beyinde bir çapa görevi görüyor ve insanların cevaplarını bilinçaltından etkiliyor. Aynı soru doğrudan en ağır insan kaç kilodur şeklinde sorulduğunda ise çok daha gerçekçi cevaplar alınıyor.
Bu örnekler çapa etkisinin bilinçaltında oynadığı rolü açıkça ortaya koyuyor. İki farklı gruptaki insanlardan soru içerisinde bir sayı verilen grup çapa görevindeki bu sayıya daha yakın tahminlerde bulundu. Sayı verilmeden fikri sorulan grup ise böyle bir etki yaşamadı.
Bu insanlar verilen çapa sayının gerçek olmadığının gayet farkındaydı. Ancak beyinleri kişilerin bilinci dışında cevabı hesaplamak için bu sayıdan faydalanma yöntemine gitti. Böyle bir yöntemin pazarlık gibi süreçlerde oldukça güçlü bir etkisi olabilir. Örneğin bir satıcı müşterisine satmak istediği fiyattan yüksek bir sayı verip müşterinin aklında bu sayı ile çapa etkisi yaratabilir. Böylece müşteri pazarlık yapsa bile ürünü normalde alacağı fiyattan yükseğe alacak.
Bu yöntemin fiyat pazarlığı konusundaki etkisi araştırmalarda yine kendini gösteriyor. Örneğin 19.95 gibi spesifik fiyatlar 20 gibi yuvarlanmış fiyatlardan daha çok satabiliyor.
Bu araştırmalardan alıntılayacak olursak:
‘Araştırmalarımız gösteriyor ki spesifik fiyatlar (29.75 gibi) yuvarlanmış fiyatlardan (30 gibi) daha güçlü bir etki yaratıyor. Ancak bu sadece Grice’ın “İşbirliği İlkesi”ndeki gibi karşılıklı bir diyaloğun sürdürülmesinde katkıları gözlemlenebilen bir insan tarafından sunulursa işe yarıyor. (Grice işbirliği ilkesi tanımı şöyle: “Söyleyeceğinizi, konuşmanın amacı ve yönü doğrultusunda, gereken zamanda ve gerektiği kadar söyleyiniz.”)
Sayılar iletişim amacından mahrum olan otomatikleşmiş bir prosedür ya da kesinlik seviyesi tahmin görevi ile pragmatik anlamda alakasız olarak sunulduğunda sayısal kesinliklerin çabasının boşa çıktığı görülüyor’
Temel oran yanılgısı
Bu yanılgı beynin temel oranını sık sık görmezden gelerek ortaya çıkardığı yanılgı ile alakalıdır. Bu tip bir yanılgıda beyin spesifik bilgilere odaklanır. Ancak bu sefer de temel oranlarını ya da daha genel bilgileri unutmaya meyilli hale gelir.
Temel oran yanılgısına bir örnek:
Bir şehirde iki renk araba olsun: Bu arabaların %85’i mavi, %15’i yeşil renkte. Bu şehirde bir vur-kaç olayı yaşanıyor. Bir görgü tanığı var. Bu tanık ifadesinde vurup kaçan aracın rengini “yeşil” olarak gördüğünü söylüyor. Yapılan testlerde bu kişinin iki rengi aynı ışık koşullarında %80 oranında doğru ayırt ettiği görülüyor. Bu koşullar altında, suçlu arabanın yeşil renk olma olasılığı nedir?
Temel oran yanılgısı hakkında hiçbir şey bilmiyorsak, cevabı % 80 diye veririz. Oysa cevap bundan çok daha düşüktür. Doğru yanıt % 41 olmalıdır. Normalde bu tip sorular Bayes teoremi ile çözülmektedir. Ancak biz teoreme girmeden sezgisel olarak cevaba ulaşalım.
Bu şehirde 100 tane araç olduğunu düşünelim. Bu durumda 85 tane mavi renkli, 15 tane de yeşil renkli aracımız var. Bu durumda tanığımız 85 mavi aracın 85 x 0.8=68 tanesini mavi olarak görecek. Benzer bir biçimde 85 x 0,2= 17 tanesini de hatalı bir biçimde yeşil olarak görecektir.
Öte yandan, 15 yeşil aracın 15 x 0.8=12 tanesini yeşil görürken, 15 x 0,2 = 3 tanesini de hatalı olarak mavi olarak görecektir. Bunlara göre tanığımızın yeşil gördüğü araçların toplamı 12+17=29 tanedir. Ancak gerçekte sadece 12 tanesi yeşildir. Bu durumda 12/29 oranını alırsak yaklaşık yüzde 41 sonucuna ulaşırız.
İnsanlar bu bilgiyi temel oranına kıyasla daha geçerli olarak kabul ediyorlar.
İnsanlar sıklıkla alakasız bir bilgiye odaklanarak istatistiksel verileri göz ardı ediyorlar. Bu da zaman zaman kafa karıştıran sonuçlara neden olabiliyor.
Bağlaç Yanılgısı ve Linda problemi
İstatistik olarak aslında yanlış olsa da beyin spesifik bilgileri genel bilgilere kıyasla daha olası görmeye meyillidir. Bu tip durumlarda verilen tanımın temsil edilebilirliğine bakılır ancak varsayımsal bir senaryo içerisinde olasılık yönü hesaba katılmaz. Bu durum ise bağlaç yanılgısına yol açar.
Bağlaç yanılgısı özellikle insanlar izlenimlerine fazla güvendiği ve durup büyük resmi değerlendirmeyi ihmal ettiklerinde oluşur.
Örnek olarak, Daniel Kahneman kitabı ‘Yavaş ve Hızlı Düşünmek’ içerisinde şöyle diyor:
‘Şöyle bir senaryo düşünün: Linda 31 yaşında, bekâr, açık sözlü ve oldukça zeki birisi ve felsefe bölümünden mezun olmuş. Bir öğrenci olarak ayrımcılık ve sosyal adalet konularında oldukça ilgilenmiş ve ayrıca nükleer karşıtı eylemlere katılmıştır.’
Aşağıda verilen durumlardan hangisi Linda için daha olasıdır:
- Linda’nın bir banka memuru olması.
- Linda’nın hem bir banka memuru hem de aktivist bir feminist olması.
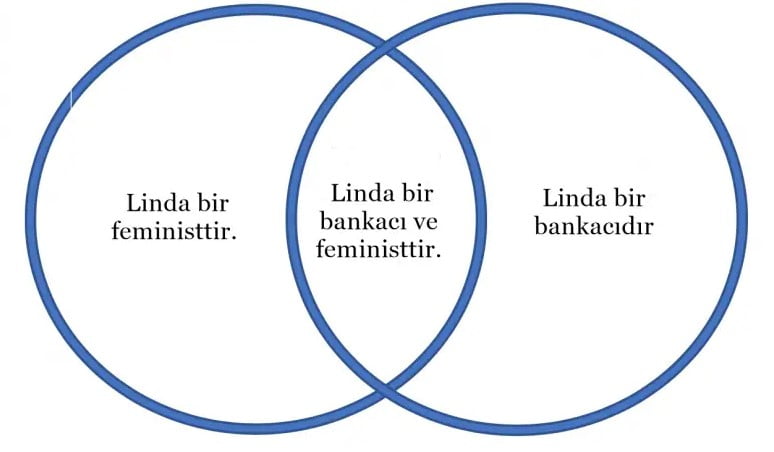
Ne düşünüyorsunuz?
Eğer siz de çoğu insan gibi düşündüyseniz muhtemelen 2. Seçeneği seçmişsinizdir. Ancak verilen durumlara dikkatli bir şekilde tekrar bakın. İstatistiksel olarak bir insanın banka memuru olması mı daha olasıdır yoksa hem banka memuru hem de aktivist bir feminist olması mı?
Fark ettiğiniz üzere ilk durum daha genel ikinci ise daha spesifiktir. 2. Durumu daha olası gören kişiler burada bağlaç yanılgısına düşmüş oluyor. Genel popülasyona baktığımızda her zaman banka memuru sayısı hem banka memuru hem de aktivist feminist olan kişi sayısından fazla olacaktır. Yani ilk durum daha olasıdır.
İnsanlar istatistikler konusunda oldukça kötüdür. Bunun sebebi ise A gerçekleşti çünkü B yüzünden gibi basit açıklamaları anlamada istatistikleri anlamadan çok daha iyi olduğundandır. Hikayeciliğin insanları ikna etme ya da harekete geçirme gücü de buradan gelir aslında. İnsanların bir bağ kurabileceği göreceli daha basit ve sıradan senaryolar onları etkilemekte daha başarılıdır.
İnsanların istatistik konusundaki yetersiz bilgisinden kaynaklanan başka bir yanılgı ise kumarbaz yanılgısıdır. Bu yanılgı her ne kadar birbirinden bağımsız olsa da geçmişteki olayların gelecekteki olayları etkilediğine sıklıkla inanan insanlar üzerinden tanımlanabilir.
Yapılan bir deneyde madeni bir para 5 kere havaya atılıyor ve hepsi tura geliyor deneklere bir sonraki seferin ne geleceği sorulduğunda ise çoğunluk yazı geleceğini düşündüklerini belirtiyor. Çünkü beyinde çoktan 5 kere tura geldi artık yazı gelecektir şeklinde bir düşünce süreci oluşuyor.
Ancak bu paranın herhangi bir şekilde hileli olmadığını varsayarsak bu düşünce yanlıştır. Önceki sonuçlardan bağımsız olarak yazı ya da tura olasılığı %50 şeklindedir.

Bu yanılgı ismini kumarhanelerde sıklıkla gözlemlenmesinden almıştır. 1913 Monte Carlo’daki bir kumarhanede geçen bir hikayeye göre rulet oyunu sırasında top üst üste tam 26 kere siyaha düşmüş! Sonuç olarak kumarbazlar bu kumarbaz yanılgısına yenik düşerek milyonlarca frank kaybettiler.
Rulet masasının etrafında dizili insanlar arka arkaya gelip duran bu siyahın sonucun kırmızı çıkma olasılığını arttırdığı yanılgısına düştü ve bu yüzden paralarını kırmızıya yatırıp durdular. Kumarbazların büyük çoğunluğu evlerine büyük kayıplarla döndü. Bu yanılgı kumarhanelerde sıklıkla meydana geliyor.
Bölüm 1’e geri dönmek için buraya tıklayın. Bölüm 3’e devam etmek için buraya tıklayın.
Çevirmen: Barış ARICAN









